德国HBM传感器的动态特性

在实际测量中，德国HBM传感器的输入可能是变化较快的连续信号，也可能是冲击输入或周期性输入。此时传感器中的各种类型的储能元件引起的暂态过程所表示的特性，与静态特性有很大差别。输出和输入之间的关系将是一个随时间变化的函数。为此，需要研究传感器的动态特性和指标。

德国HBM传感器动态特性的描述和分析方法与一般控制系统中常用的方法相同，但侧重点有所差异。在一般情况下，传感器可以看作一个动态复现系统，对这种系统的要求是在动态工作条件下（输入为随时间变化的函数），从最小的误差复现输入作用。

2.3.1频率特性及其动态品质之间的关系

线性系统在正弦输入作用下输出幅值与输入幅值的比值称为系统的幅频特性，以 | H（j ω）| 表示，而输入与输出之间随频率而变的相位特性称为相频特性，以 φ（ω）表示 。图2-4所示为一典型的幅频和相频特性，统称频率特性。

频率特性是德国HBM传感器的一个十分有用的评估特性，用于评价传感器在波形复杂的周期输入作用下的复现误差。

理论证明，在图2-4中，幅频特性呈线性区间是 ０ ＜ ω ＜ ω１。由于幅频特性平坦，对所有落在此区间内的谐波输入都有相同的灵敏度，因而不产生幅值误差。而线性变化的相频特性，可以保证不出现的各种谐波所组成的任意复杂波形都能被精确地复现。由此可以得出结论：频率特性的形状对评估动态误差有重要意义。

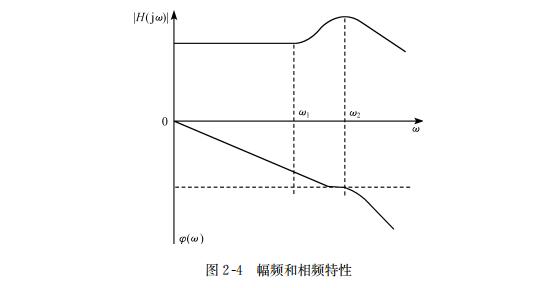
同样可以证明：固有频率拓宽，则在指定精度下的平坦区间也将拓宽。因此，通过改变传感器的固有频率可以改变动态范围。

最后，频率特性与时间响应之间有着确定的关系，通过频率特性可以计算暂态响应。从典型环节的频率特性，可以了解结构参数对它的影响及暂态响应之间的关系。

1.一阶德国HBM传感器

具有简单能量变换的传感器，如多数物性型传感器，其动态性能可以用一阶微分方程来描述。直接利用微分方程或传递函数，可以得到典型的一阶传感器的频率特性，即

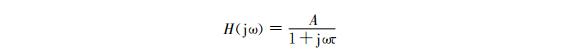
相应的幅频和相频特性为

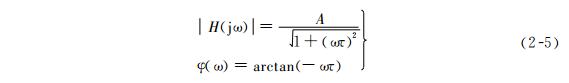
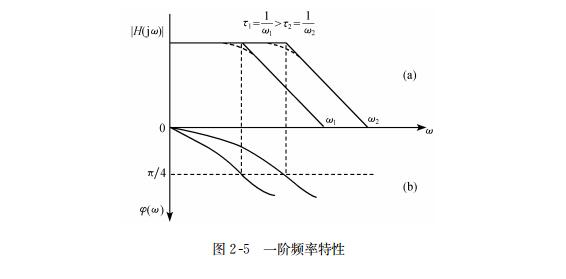
其图形以对数坐标示于图2-5。由图可见，一阶频率特性具有最简单的形式，其特征参数可用 ３dB 频率 ωc 表示，即

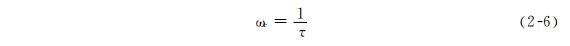
此处，τ称为传感器的时间常数。由图可见，时间常数 τ越小，则 ３dB 频率 ωc 越高，具有较好的动态响应。或者说，较小的时间常数响应较快。

2.二阶德国HBM传感器
                                                       

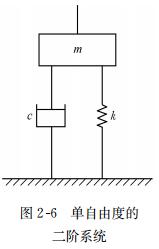
众所周知，在电气系统中具有R、L、C 的电路呈现二阶频率响应。同样，对于具有阻尼、质量和弹簧的机械系统（图2-6），如测力和测量震动的传感器，也有类似的特性。根据力平衡原理，可列出微分方程

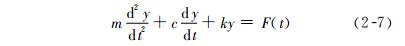
由此可得出频率特性

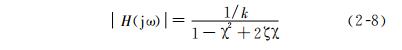
式中，χ 为频率比，χ ＝ ω／ ω ０；ω ０ 为系统无阻尼时的固有频率 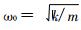，；ζ为比阻尼系数， 。

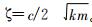由式（2-8）可分别求得幅频和相频特性，其相应的图形示于图2-7。

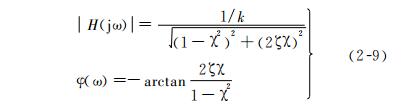
由图可见，频率特性与两个参数有关，即无阻尼的固有频率 ω０（在 χ ＝ １ 处）和比阻尼系数ζ，同时可以看出谐振峰值大小和谐振频率 ω n 随 ζ 而变化 ，对式（2-9） 进行微分，并使之等于零，可得

              

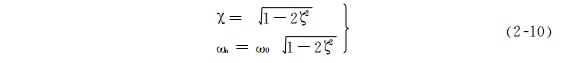
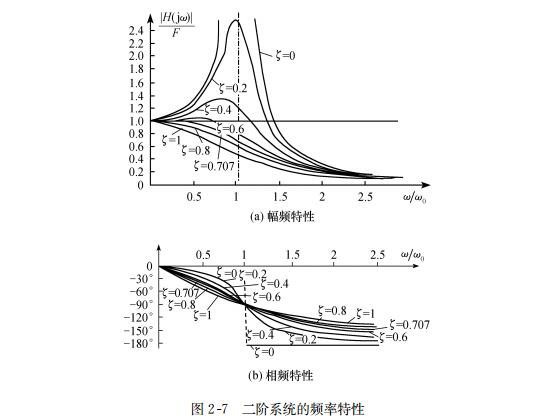
由此可见，在 ζ ＜ 0.707 时，在某一ω０下出现谐振。在ζ＝0.707处，ωn ＝０，就不再出现谐振峰，此状态称为临界阻尼状态。

由图形和计算都可表明：二阶系统的频率特性可以用两个特征参数 ω ０ 和 ζ来评估 ：在相同的 ζ下，ω０ 越大则特性的平坦区越大，动态特性越好；在确定的固有频率下，当 ζ ＝ 0.707时，具有最宽的幅频特性平坦区。

2.3.2时域响应特性和动态品质指标

在时域中分析动态响应特性是一种直观的方法，可给出评估动态误差的清晰的概念。在快变的输入作用下，传感器的输入与输出之间的关系是一个随时间变化的关系。产生这种现象的原因是由于输入作用引起的系统的暂态分量的影响。因此，系统在动态下的输出，可以看作是由两个分量构成：第一个分量是像静态特性一样与输入保持确定的关系；第二个分量是由输入作用引起的暂态分量，也叫动态误差。

显然，暂态分量反映了传感器中能量的存储（电场、磁场、位能、动能及热积累等）过程和消耗（电阻、摩擦等）过程之间的动态平衡关系。用典型的输入作用，就可以观察到它们之间的关系，最常用的典型输入作用是阶跃函数 。图2-8表示在零初始条件下具有代表性的阶跃响应曲线。图中 y（ ∞ ）表示暂态结束后的稳态值，它与输入 x（t）的关系由静态特性确定。由图可见 ， 暂态分量的影响只是在前沿部分显示出来，故传感器的动态品质参数，可用阶跃响应的前沿部分的某些特征来表示 ， 常用的有如下几种（图2-8）：

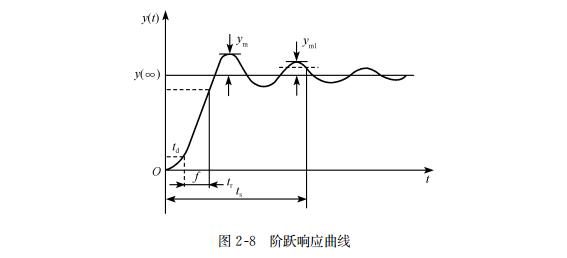
① 时滞。从阶跃输入开始，到输出响应开始变化为止的时间间隔，以 td 表示。

② 上升时间。为了排除时滞的影响，上升时间的开始点定为输出响应达到某一百分值 （稳态值的5%或10% ）处，而终点是输出第一次达到稳态值的某一百分值 （如90% ）处。显然此段时间间隔与规定的两个百分比有关，以 tr 表示，并给出相应百分比 。

③ 阶跃响应时间。从阶跃输入开始，输出值第一次达到稳态值的规定误差范围所需的时间，常以 ts 表示，并与规定误差一同给出，如 ts（５ ％ ）。显然 ，ts包括时滞。

④ 瞬时过冲。对于阶跃响应，输出值超出稳态值的最大瞬时偏差 ym ，并将此偏差用稳态值的百分数表示，如 。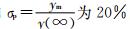

⑤ 衰减度。用来描述振荡的阶跃响应衰减的速度，以 φ 表示。其值用相邻两次过冲幅值差（ ym１－ym２ ）与 ym１ 的百分比来表示，φ 越大，表示衰减越快。

⑥ 稳定时间。描述了暂态过程从开始到结束的整个时间，以 ts１ 表示。为规定暂态的结束（理论上可能要无穷大时间，需规定一个稳态误差ε。稳定时间就是从阶跃输入开始，到输出响应最终进入规定误差范围内所需要的时间。

由上述可见，德国HBM传感器的动态性能可用一个或几个参数来描述。其描述方法与传感器的暂态过程的特点有关。例如，对单调的过程和衰减振荡的过程描述，可能就大不相同。下面就暂态过程的特点，讨论两种典型过程。

1.单调变化的阶跃响应

由多个惯性环节组成的开环系统，其阶跃响应呈单调变化，可用上升时间、阶跃响应时间或稳定时间三者之一来描述其性能。对简单的只有一个惯性环节的系统，只需给出时间常数，阶跃响应可立即完全确定，见图2-9，有

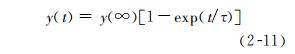
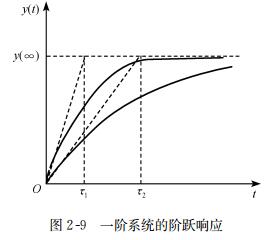
由图可见，τ越小，响应时间和稳定时间越小，动态性能越好。和式（2-6）相比较可以看出，τ小意味着频带变宽。

2.典型的二阶系统

二阶系统的传递函数可由式（2-7）求得，即

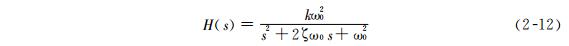
图2-10表示二阶系统的阶跃响应曲线，图中 ζ ＝0.707的曲线表示临界阻尼状态。比较三条曲线可以看出，临界阻尼具有最小的稳定时间，ζ 越小则上升时间越短。从响应时间角度看来，临界阻尼并不是最佳状态。分析表明： ζ 越小则瞬时过冲量越大，因此实际中一般选择 ζ为0.5～0.7，以便能在允许过冲量条件下得到最小的响应时间。比较图2-7和图2-10可以看出，较小的 ζ值具有较宽的频带（３dB）带宽，故上升时间与带宽有关 。

★ 德国HBM：称重传感器-- Z6F,C16I,C16A,RTN,HLCB1, PW2D,PW6D,PW2C,PW6K,PW6C,PW10A,PW12C,PW16A,PW22,S40A,C2等系列
★ 德国HBM：扭矩/力传感器 -- T40B,T22,T5,U9C,C9C,S9M,U2B,S2M等系列
★ 德国HBM：称重仪表/变送器 -- WE2111,RM4220, BM40,AE101, AE301,EM201等系列
★ 美国世铨celtron:传感器 -- STC,HBB,LPS,LOC,PSD,LCD,MBB,SQB等系列
★ 特迪亚Tedea-huntleigh: --3410，616，355，1015，1040，1022，1260，120，1241，240等系列
★ 美国传力Transcell ：传感器-- BSS,BSH,DBSL,SBST,CR,SBS,BAB等系列
★ 梅特勒托利多：称重传感器--  TSC，TSB，MTB，GD，SLB415，SLB215，MT1022，MT1260，MT1241，SB，SBS，SBH等系列
★ METTLER TOLEDO：数字传感器—GDD,SLC720,0760,PDX，SLC820等系列
★ 梅特勒托利多：控制仪表 -- IND331，IND245，IND320L，IND230，IND560，B520，IND110，WM0800，AJB等系列
 
联系人：黄浩   电话：18688492451（微信同手机号）